Chainerのソースを解析。MNISTサンプルを追ってみる


勉強のつもりで Chainer の公式サンプル MNIST のソースを追ってみました。
バージョンは 1.14.0 、2016年9月5日時点のソースです。

参考書としてお世話になったのが「深層学習 (機械学習プロフェッショナルシリーズ)」です。横に置いて、あれこれ確認しながら python のコードを追っかけました。

文中では 青本 と呼ばせていただきました。

- 目次 -

スポンサーリンク

MNISTとは

手書きの数字を画像化したデータ集で 70,000件のデータが用意されています。画像データと同時に正解ラベルも提供されており、機械学習の評価用データとして幅広く利用されています。
THE MNIST DATABASE

Chainerのサンプル構成

サンプルを構成するのは 2 ファイルです。

mninsit_sample
  • train_mnist.py
    全体の流れ（データ取得 ～ モデル生成 ～ 学習ループ）を記述
  • mnist.py
    データの取得

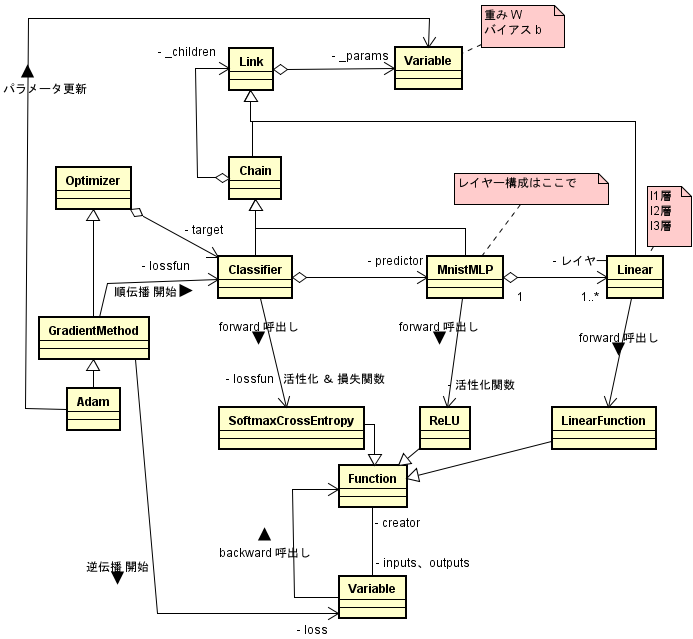
クラス図

MNIST に関わるクラスを抜き出して図にすると
mnist_class

まずは train_mnist.py

train_mnist.py に main 関数があります。処理の流れとしては

  1. モデルの生成
  2. オプティマイザの生成
  3. 学習・テストデータのダウンロード
  4. trainer、updater の生成
  5. extension の登録
  6. 学習ループ

といった感じです。

モデルの生成

MNISTのサンプルは、全結合を 3 層ならべて、中間層には活性化関数 ReLU、出力層にはソフトマックス関数を適用し、クロスエントロピーで損失を求めています。ユニット数は下図のとおり、1000、1000、10 です。
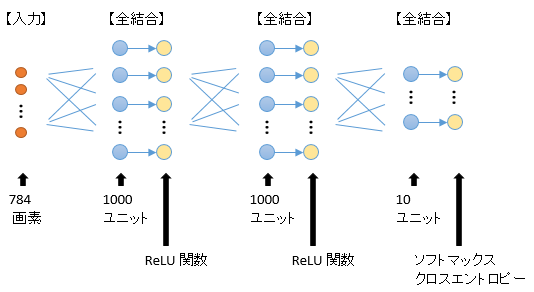
mnist_unit
出力層（図の右端）の各ユニットは、以下の確率を出力します。

【ユニット】
1
2
：
10
【確率】
入力画像が 0 である確率
入力画像が 1 である確率
      ：
入力画像が 9 である確率

この構成を、プログラムでどのように実装しているのか見ていきます。

モデル生成箇所

train_mnist.py の 53行目でモデルが生成されます。
model_create
Classifier、MLP といったクラスが登場しています。
何者でしょうか。

レイヤー構成を定義する MLP

MLP はレイヤー構成を定義するクラスで、train_mnist.py の冒頭に記述されています。

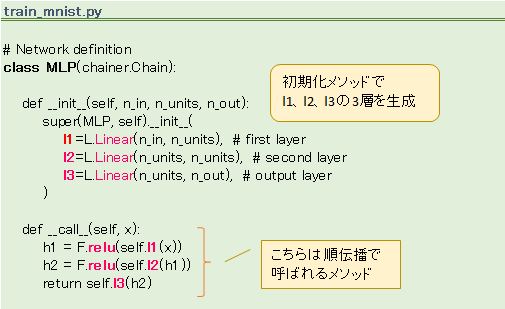
mnistmlp

__init__で、Linear クラスを 3 つ（l1、l2、l3）生成しています。全結合を実現するのがこの Linear クラスで、他のサンプルにも結構出てくる使用頻度の高いクラスです。> くわしくは、こちらで説明

Linear の引数に n_in、n_units、n_out という変数が指定されています。
この変数にはそれぞれ、784、1000、10 という値がデフォルトで渡されます。
つまり

l1=L.Linear(784,  1000)
l2=L.Linear(1000, 1000)
l3=L.Linear(1000, 10)

l1 は 784   ユニットを受け取って 1000 ユニットに展開
l2 は 1000 ユニットを受け取って 1000 ユニットに展開
l3 は 1000 ユニットを受け取って 10     ユニットに展開

1000 × 1000 × 10 のユニットがここで生成されています。

__call__のほうに目をやると、relu クラスがでてきます。これが ReLU 関数です。つまり、__call__が呼ばれると ReLU が生成されるわけですが、では、どのタイミングで__call__が呼ばれるのでしょうか。

Chainer のソースを見ていると__call__メソッドが頻繁に出てきます。この__call__メソッドには、順伝播の処理が記述されており、学習ループに入って順伝播が始まると、関連するクラスの__call__メソッドが次々、連鎖的に呼ばれる仕組みになっています。

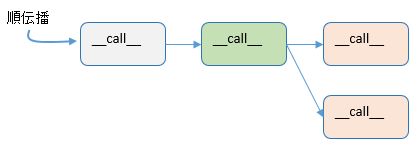
call2call

MLP の__call__も、やはり順伝播で呼ばれます。そして、その中で ReLU 関数が生成される仕組みです。

ここまでに全結合の Linear、活性化関数の relu が出てきましたが、ソフトマックス関数とクロスエントロピー損失関数が見当たりません。どこだ、どこだ？・・・ありました。Classifier クラスに出てきます。

Classifier

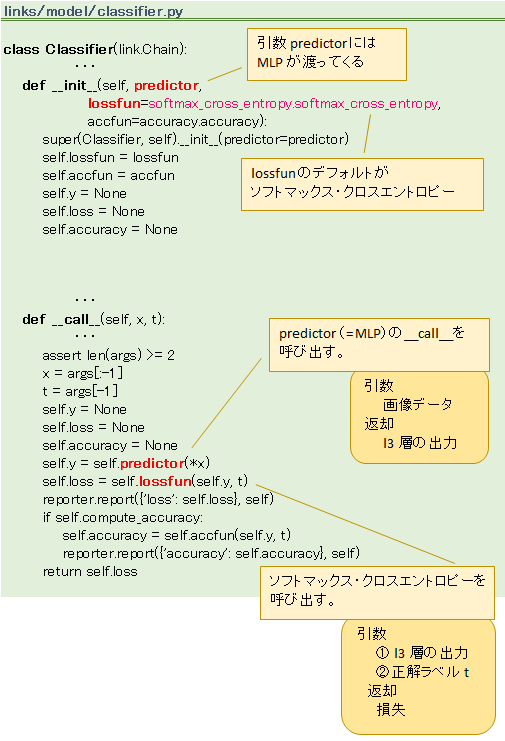
Classifier の__init__の引数 lossfun が、デフォルトでソフトマックス・クロスエントロピー関数になっています（下図 ピンク色）。そしてこの lossfun は、__call__メソッドの中で使われており、それはつまり、順伝播の処理で呼び出されることを意味します。

Classifier の__init__には引数がもうひとつあります。predictor ですが、ここには MLP がセットされます。
classifier

モデルのインスタンス

Linear のインスタンスは内側に重みやバイアスを持つので（詳しくはこちらで）、モデルの初期化の段階で

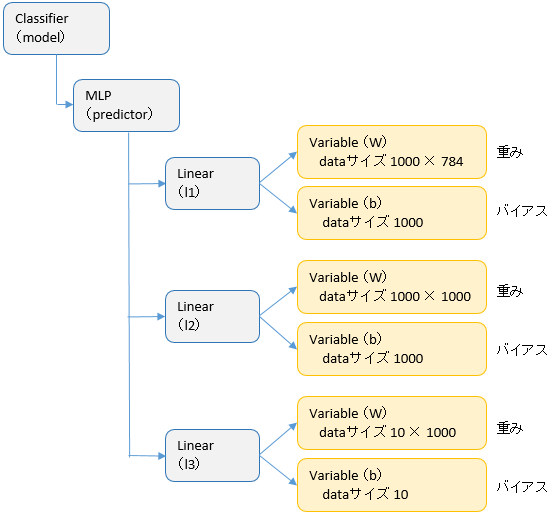
mnist_init_model

こんなインスタンスができあがります。

縦に 3 つ並んでいるのが Linear 、つまり全結合層、右横の Variable が重み（W）とバイアス（b）です。ReLU や ソフトマックス・クロスエントロピー関数は初期化の段階ではインスタンス化されません（学習ループに入って順伝播が始まってからインスタンスが生成されます）。

Classifier インスタンスは、プログラム上では変数名 model と名付けられています。この model にデータを渡すと順伝播が始まります。

model の生成が済んだらオプティマイザの生成へと移ります。

オプティマイザの生成

オプティマイザの役割は重み・バイアスの更新です。model によって順伝播・逆伝播が実行され勾配が計算されますが、その値を重み、バイアスに反映するのが仕事です。その役割上、model をラップするような形になります。
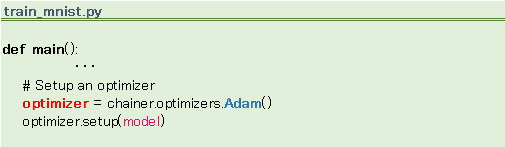
optimizer_in_main

Adam ？

重み・バイアスの更新にはさまざまな手法があり、その手法に応じてオプティマイザの具象クラスが複数用意されています。MNISTのサンプルは Adam アルゴリズムを採用しており、使用するクラス名も、ずばり Adam クラスです。


オプティマイザの生成が済んだらデータをダウンロードします。

学習データ、テストデータのダウンロード

MNIST のデータはプログラムが自動でダウンロードしてくれ、データは以下の形で保持されます。画像の画素数は 784 です。

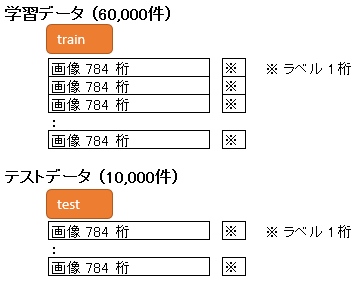
mnist_data

ソースは 63 行目から

mnist_data

◇◇◇

ここまでが、いわば初期化です。初期化がすむと、いよいよ、学習ループに入ります。

学習ループ

以前の chainer は学習ループをアプリケーション側 （MNIST の場合は train_mnist.py） に記述していましたが、その後の改変で、学習ループはフレームワーク内部に隠蔽されました。隠蔽先は Trainer クラスです。
Trainer クラス内部にループがあり、そのループの内部で順伝播と誤差逆伝播を繰り返すのですが、ここに Updater というクラスも関わってきます。
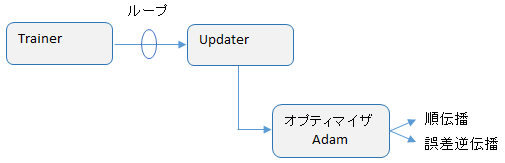
loop_src
main() からの流れをソースで追ってみます。
Trainer の run メソッドを呼び出すと学習が始まります。
loop_src

main() → Trainer.run() → Updater.update() → Optimizer.update() の順で処理が移行し、オプティマイザの update メソッドの中で

順伝播 → 逆伝播 → 重み・バイアス更新

が順次行われます。

順伝播

では、順伝播から見ていきます。

順伝播の処理をおおまかにわけると

  • ① 入力に重み・バイアスをかけあわせる
  • ② 活性化関数を適用する
  • ③ 損失関数を適用する

の 3 つになります。

①②③ともロジックがいろいろあり、それぞれ対応クラスがありますが、 MNIST で使用するクラスは

  • ① LinearFunction
  • ② ReLU
  • ③ SoftmaxCrossEntropy

です。

呼出し経路

①②③ に共通するのは、どれも Function の具象クラス という点です。

Function の具象クラス には foward と backward という具象メッソッドが定義されており、順伝播に相当する foward のほうは__call__経由で呼び出されます。

オプティマイザの update 以降は下図のように呼び出されます。
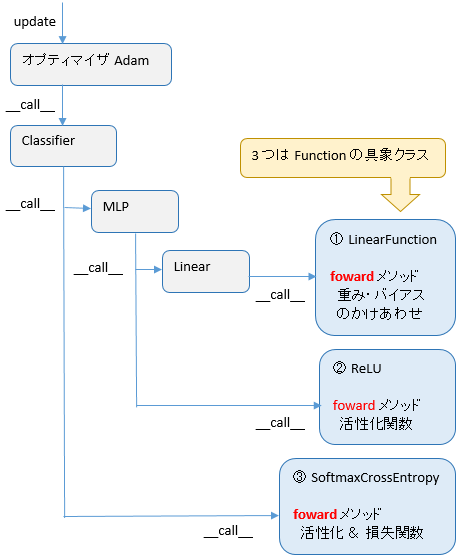
mnist_foward

Function は入力も出力も Variable

学習データをふくめ、Function の入出力データはすべて Variable です。そして、ある Function が出力した Variable は、後続 Function の入力となります。
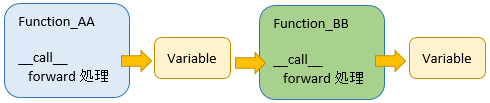
func_var

インスタンス状態

重みやバイアスも Variable ですから順伝播のあとの各クラスのインスタンスは下図のようになります。
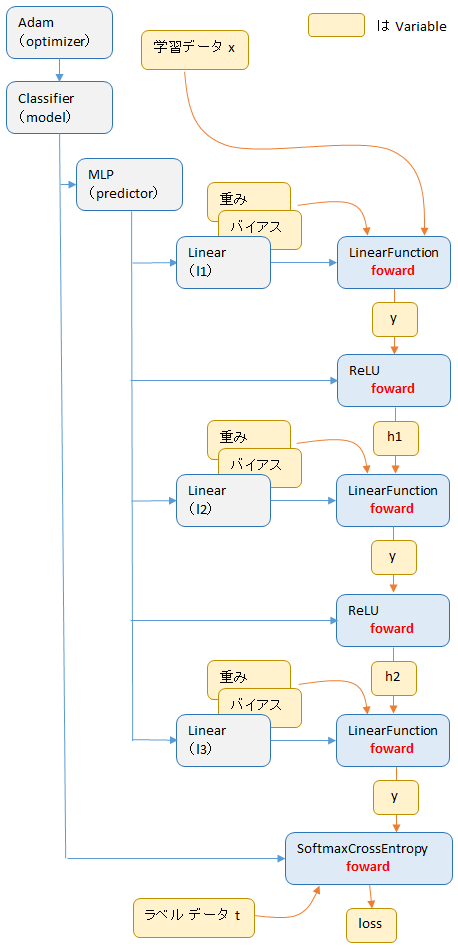
instance_after_learn

では、各 Function の foward 処理について、その中身を見ていきます。

LinearFunction の foward 処理

LinearFunction の foward メソッドで、入力に重みとバイアスをかけ合わせます。
linear_f_src
l1層を例にとると、784 画素の入力 x に対して、下図のように重みをかけてバイアスを加算し、結果 1000 ユニットの出力 y を作成します。

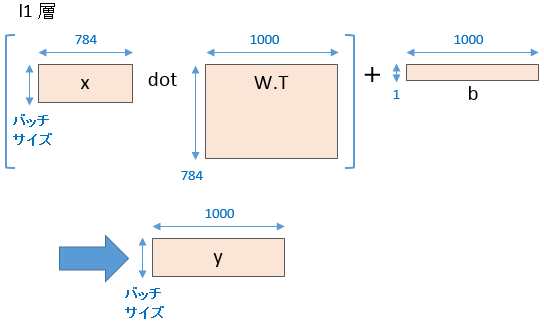
foward_l1

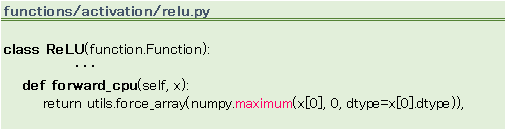
ReLU の foward 処理

ReLU は 青本の表 4.1 に出てくる正規化線形関数で、l1 層、l2 層の活性化関数になっています。
計算式は

\(f(u)=\max(0,u)\)

です。
relu_f_src
l1 層、l2 層ともに、ReLU への入力は バッチサイズ × 1000 です。したがって、下図のような計算を行います。

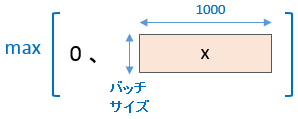
li_relu

SoftmaxCrossEntropy の foward 処理

l3 層の活性化 ＆ 損失関数です。

活性化 のほうは ソフトマックス関数

\(\Large{\frac{\exp(u_{k}^{(L)})}{\sum_{j=1}^K \exp(u_{j}^{(L)})} }\)    （青本の式（2.9））

損失 は 交差エントロピー

\(-\sum_{n=1}^N \sum_{k=1}^K d_{nk}\log y_{k}(x_{n};w)\)    （青本の式（2.11））

で求めています。

入力 x （上式の \(u\)） のサイズは
softmax_x
です。

softmax_f_src

  • self.y は、逆伝播で使用されます。
  • y はこの関数の戻り値となり、評価に使用されます。

ソフトマックス関数の計算

self.y の計算過程がちょっとわかりにくいですが、あちこち関数で処理して、こうなっています。

まず \(m=\max(x)\) と置いて

\(\large{self.y}\)
\(=\exp \left(x-\left(\log \sum_{j=1}^{10} \exp (x_j-m)+m \right) \right)\)     ※括弧の中身が log_y
\(=\Large{\frac{\exp (x)}{\exp \left(\log \sum_{j=1}^{10} \exp(x_j-m)+m \right)}}\)
\(=\Large{\frac{\exp (x)}{\sum_{j=1}^{10} \exp (x_j-m) \times \; \exp(m)}}\)
\(=\Large{\frac{\exp (x)}{\sum_{j=1}^{10} \exp (x_j)}}\)

誤差逆伝播

つづいて逆伝播をみていきます。
逆伝播の処理は、順伝播で生成したインスタンスを逆からたどるように行います。
> くわしくは、こちらで説明

勾配の計算式

勾配を求める数式を青本から引用します。式（4.9）です。
ex4_9
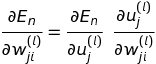
この式を展開して、いろいろやると
loss_formula
となります。導出については青本を参照してください。

ポイントとなるのは各層のデルタ（\(\delta \)）です。
デルタを上位層から下位層に引き渡し、そこにレイヤー入力値（\(z_i^{(l-1)}\)）を積算して勾配を算出しますが、プログラムでは実際、どのように処理しているのでしょう。

勾配、デルタの置き場所 grad

Variable にはデータ領域が 2つあります。
data と grad です。
data_grad
逆伝播の処理では、grad に計算結果が保持されます。
計算結果とは、たとえば、勾配の値です。そしてデルタの値も grad を経由して各層に引き継がれていきます。

デルタの計算手順

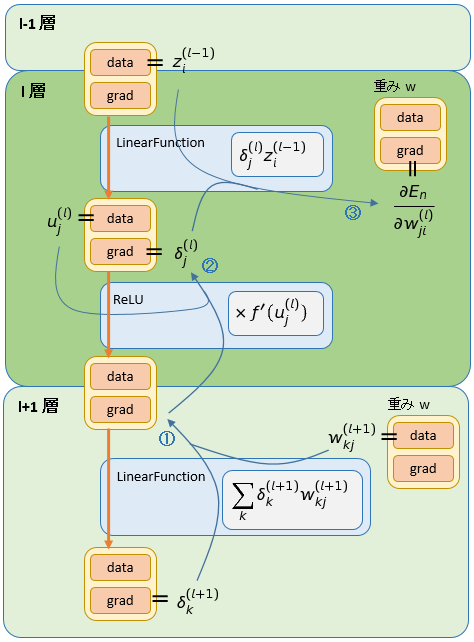
デルタの値は式（4.12）で計算しますが、この計算は 2 段階にわけて実装されています。
まず

\(\sum_k\delta_{k}^{(l+1)} w_{kj}^{(l+1)} \)

の部分を LinearFunction の backward で計算します。そして ReLU の backward で

\(f’\big(u_{j}^{(l)}\big) \)

をかけてやります。（下図の ①、② に相当）

l 層の勾配を計算

backward_flow

勾配の計算

最後の ③ が式（4.13）に相当します。

ソースで確認

LinearFunction と ReLU のソースで backward の部分を確認してみます。
linear_b_src
relu_b_src

出力層のデルタ

デルタにはもうひとつ、出力層のデルタというものがあります。上に書いたのは中間層のデルタの求め方で、出力層ではそれとは別の計算式でデルタを求める必要があります。
青本の 4.4.1 項にその計算式がのっています。

\(\delta_j=y_j-d_j\)

\(y_j\)はユニット j の出力、\(d_j\)はユニット j の目標出力です。
たとえば、画像が「3」の場合、\(y_j\)、\(d_j\)、\(\delta_j\)の関係は
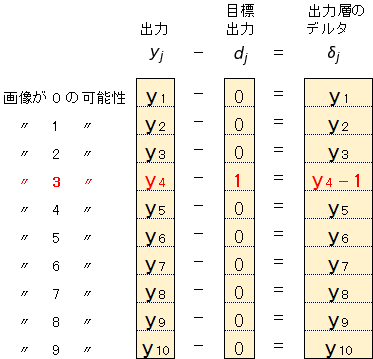
y_d_delta
となります。

上図の右端の値がほしいわけですが、これは正解に相当するユニットの出力から 1 を引けば簡単に求まります。
計算は SoftmaxCrossEntropy の backward で行います。
softmax_b_src

あとはオプティマイザが grad ⇒ data

grad にセットされた勾配は optimizer の update メソッドで data に反映されます。
> くわしくは、こちらで説明optimizer_update

スポンサーリンク
その他の記事

コメントはお気軽に