ツリーやグラフ状のデータを探索する方法に深さ優先探索と幅優先探索があります。両者の違いとプログラムの実装方法を見ていきます。
- 目次 -
スポンサーリンク
探索方法の違い
深さ優先 と 幅優先 の探索方法の違いを簡単に説明するとこうなります。
ツリー状のデータ A ~ H があるとします。
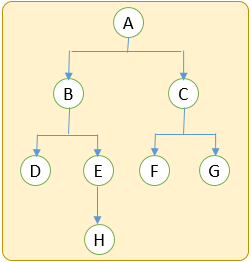
このデータを深さ優先と幅優先で探索すると、探索の順番は以下のようになります。
深さ優先
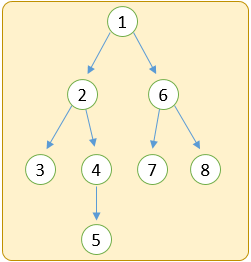
深い階層を優先して辿っていく
幅優先
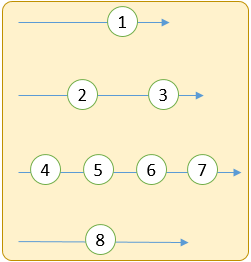
同じ階層をすべて辿ってから次の階層へ
深さ優先 は、階層の深いデータが見つかればそちらをどんどん掘り進めていきます。幅優先 は、同じ階層のデータをすべて探索し終えるまで次の階層へ行きません。
ディレクトリ探索
ディレクトリ探索の処理を深さ優先、幅優先で実装してみます。python を使います。
ディレクトリは下記のように作ってあります。
|
1 2 3 4 5 6 7 |
root ┗ a0 ┃ ┗ a0_b0 ┃ ┃ ┗ a0_b0_c0 ┃ ┗ a0_b1 ┗ a1 ┗ a1_b0 |
深さ優先
深さ優先探索は 再帰呼び出し で行います(再帰呼び出しについて)。
|
1 2 3 4 5 6 7 8 9 10 11 |
import os def dfs(path): print path for child in os.listdir(path): child_path = path + '/' + child if os.path.isdir(child_path): dfs(child_path) # 再帰呼び出し dfs('/root') |
結果
|
1 2 3 4 5 6 7 |
/root /root/a0 /root/a0/a0_b0 /root/a0/a0_b0/a0_b0_c0 /root/a0/a0_b1 /root/a1 /root/a1/a1_b0 |
幅優先
幅優先探索は、キュー を使って処理します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import os from collections import deque def bfs(path): q = deque([]) # キュー q.append(path) while len(q) > 0: p = q.popleft() # キュー取りだし(先頭) print p for child in os.listdir(p): child_path = p + '/' + child if os.path.isdir(child_path): q.append(child_path) # キュー追加 bfs('/root') |
結果
|
1 2 3 4 5 6 7 |
/root /root/a0 /root/a1 /root/a0/a0_b0 /root/a0/a0_b1 /root/a1/a1_b0 /root/a0/a0_b0/a0_b0_c0 |
再帰呼び出しを使わずに深さ優先
再帰呼び出しを使わずに深さ優先で探索することもできます。
方法
幅優先探索でキューを使いましたが、キュー を スタック に置き換えると深さ優先探索になります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import os from collections import deque def dfs_2(path): q = deque([]) # スタック q.append(path) while len(q) > 0: p = q.pop() # スタック取りだし(末尾) print p for child in os.listdir(p): child_path = p + '/' + child if os.path.isdir(child_path): q.append(child_path) # スタック追加 dfs_2('/root') |
結果
|
1 2 3 4 5 6 7 |
/root /root/a1 /root/a1/a1_b0 /root/a0 /root/a0/a0_b1 /root/a0/a0_b0 /root/a0/a0_b0/a0_b0_c0 |
スタックは先入れ後出しで動くため、再帰呼び出しのケースと順番が異って出力されます。