機械学習の解説書でディリクレ分布がちょくちょく出てきますが、なんとなく判ったような判らないような、曖昧な気分で読み流すことが多かったりします。

まず、見た目からして難しそうです。難しいので、ごちゃごちゃした

の部分は一旦忘れます。
この部分は正規化項、つまり、確率の総和が 1 になるよう調整するもので、すっきり省いて

と書いても間違いではありません。随分見やすくなります。

式の詳細に立ち入るのは大変なので、概念的な話にしぼって、ディリクレ分布は一体何を表すのかまとめてみます。

サイコロの目の出やすさ

ディリクレ分布を現実世界で例えるなら、サイコロの目の出やすさと考えるのがいいようです。サイコロを何度も投げて、その結果から各目の「出やすさ」を割り出すイメージです。

話を簡単にするため、3 面サイコロで考えてみます。

式はこうなります。

サイコロの目の数 3 は K に相当し、代入すると赤字のようになります。式をよく見ると、値 1、2、3 ごとに \(x^{\alpha-1}\) を掛けているのが分かります。この、\({\bf x}=(x_1, x_2, x_3)\) と \({\bf \alpha}=(\alpha_1, \alpha_2, \alpha_3)\) は何を表すのでしょうか。

パラメータ \({\bf \alpha}\) と \({\bf x}\)

\(\alpha\) が表すのは 1、2、3 の目の出た回数です。正確に言うと、回数に 1 を足した値です。たとえば、サイコロを 30 回投げて、1、2、3 が均等に 10回 づつ出たとします。この場合、10回、10回、10回という回数に 1 を足した値が \(\alpha\) に相当します。

そして、 \({\bf x}\) が表すのが「出やすさ」です。

「出やすさ」は無限に考えられる

1、2、3 が均等に出たなら「出やすさ」は、それぞれ【1/3、1/3、1/3】と考えるのが妥当かもしれません。しかし、断言はできません。微妙に重心がずれて、【1/3、0.9/3、1.1/3】の可能性や【1/3、0.8/3、1.2/3】の可能性も排除できません。【2.8/3、0.1/3、0.1/3】 のように偏った「出やすさ」も可能性はゼロではありません。

式に当てはめると、それぞれこうなります。

① \(\small Dir \big({\bf x}=(\ \ \ \ \ 1/3,\ \ \ \ \ \ 1/3,\ \ \ \ \ \ 1/3) \ |\ {\bf \alpha }=(11,11,11)\big) \propto \normalsize \left(\frac{1}{3}\right)^{10} \left(\frac{1}{3}\right)^{10} \left(\frac{1}{3}\right)^{10}\)
② \(\small Dir \big({\bf x}=(\ \ \ \ \ 1/3,\ \ \ 0.9/3,\ \ \ 1.1/3) \ |\ {\bf \alpha }=(11,11,11)\big) \propto \normalsize \left(\frac{1}{3}\right)^{10} \left(\frac{0.9}{3}\right)^{10} \left(\frac{1.1}{3}\right)^{10}\)
③ \(\small Dir \big({\bf x}=(\ \ \ \ \ 1/3,\ \ \ 0.8/3,\ \ \ 1.2/3) \ |\ {\bf \alpha }=(11,11,11)\big) \propto \normalsize \left(\frac{1}{3}\right)^{10} \left(\frac{0.8}{3}\right)^{10} \left(\frac{1.2}{3}\right)^{10}\)
④ \(\small Dir \big({\bf x}=(\ \ 2.8/3,\ \ \ 0.1/3,\ \ \ 0.1/3) \ |\ {\bf \alpha }=(11,11,11)\big) \propto \normalsize \left(\frac{2.8}{3}\right)^{10} \left(\frac{0.1}{3}\right)^{10} \left(\frac{0.1}{3}\right)^{10}\)

計算すると、① > ② > ③ > ④ になります。
このディリクレ分布の値は何を意味するのでしょうか。

「出やすさ」\(x_1, x_2, x_3\) の合計は必ず 1 になりますが、その条件を満たす組合せは無限にありえます。つまり「出やすさ」の候補は数限りなく存在し、どれかひとつに絞ることはできません。
ただ、そうはいっても、候補のなかには有力な候補もあれば、ちょっとありえない候補もありさまざまです。各候補がどのくらい有力か、それを数値として表すのがディリクレ分布の値 ①②③④です。（確率密度のことです。うまく表現できてませんが）

実際の値を見てみます。

python の scipy で値を計算

python の scipy に dirichlet があり、ディリクレ分布の値を計算してくれます。

x=(0.333, 0.333, 0.334) のほうが有力であることがわかります。

プロット

図にプロットしてみます。
が、その前に確認事項が 1 点。

\(x_1, x_2, x_3\) の範囲

サイコロの目 1、2、3 の「出やすさ」は \(x_1+ x_2+ x_3 = 1\) が前提ですから、各値は下記の三角形のどこかに必ず位置します。

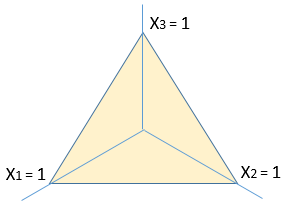
言い方を変えると、この三角形の内側は、全ての点が「出やすさ」に相当します。
そして、全ての「出やすさ」に対してディリクレ分布の値 \(Dir \big({\bf x}=(x_1,x_2,x_3) \ |\ {\bf \alpha }\big)\) が存在し、「出やすさ」としてどのくらい “有力” かが示されます。

したがって、ディリクレ分布をプロットすると、三角形を底辺とする 3 次元グラフになります。当然 3D で描くと判りやすいのですが、大変なのでここでは等高線で描画します。

等高線

プロットすると下記のような等高線になります。

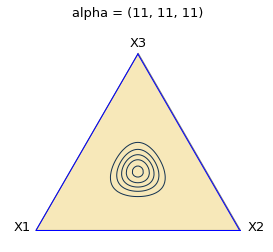
\(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\) をピークにした山状になっています。つまり「出やすさ」は \(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\) 周辺と考えるのが妥当で、そこから離れるにつれ、徐々に「ありえない」出やすさになっていきます。

ここで、回数を倍にしてみます。サイコロを 60 回投げて、20 回づつ均等に目が出た場合です。

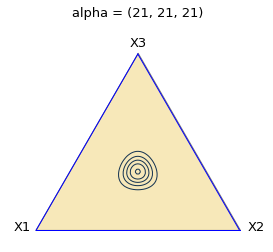
ピークは同じく \(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\) ですが、山が急になっています。これはつまり、30 回投げた結果より 60 回投げた結果のほうが、「出やすさ」の予想が絞られたと考えることができます。

回数をふやしていくと、どんどん急になります。

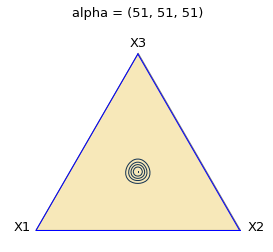
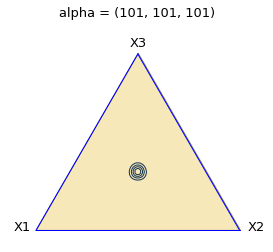
目が均等でない場合

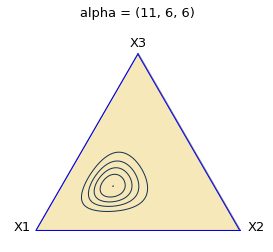
サイコロの結果が均等ではない場合、たとえば、1、2、3 がそれぞれ 10 回、5回、5回出た場合、等高線はこうなります。