目的地までの経路が何通りもあるような設定で、動的計画法(dynamic programming)を使って最短経路をもとめてみます。
考え方
例題
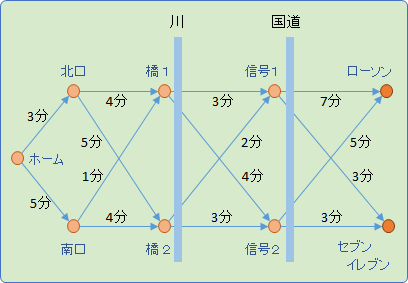
現在地は左端、駅のホームにいます。
目的地は右端のコンビニ (ローソン または セブンイレブン) です。
とにかく急いで買い物がしたいので、最速でいけるコンビニに向かいたいとします。
どちらのコンビニに、どんな経路で行くべきでしょうか。
もちろん しらみつぶしに時間を計算してもいいのですが(2 の 4乗で16通り)
なるべく計算量を減らす工夫をします。それが動的計画法です。
計算のコツ
一度に全体の経路を考えず
- ① 川までの最短
- ② 国道までの最短
- ③ コンビニまでの最短
と順番に考えていきます。
そして、① の結果をもとに ② をもとめ、② の結果をもとに ③ をもとめます。
手前から順に最短をもとめていく
① 川 (橋1、橋2) まで
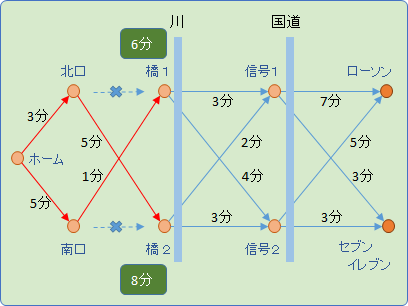
まず、川 (橋1、橋2) までの最短経路をもとめます。
▲ 橋1
ホーム → 北口 → 橋1 : 7分 (遠回り。この経路は選択肢からはずす)
ホーム → 南口 → 橋1 : 6分 ⇐ 橋1への最短経路
▲ 橋2
ホーム → 北口 → 橋2 : 8分 ⇐ 橋2への最短経路
ホーム → 南口 → 橋2 : 9分 (遠回り。この経路は選択肢からはずす)
するとこうなります。
② 国道 (信号1、信号2)まで
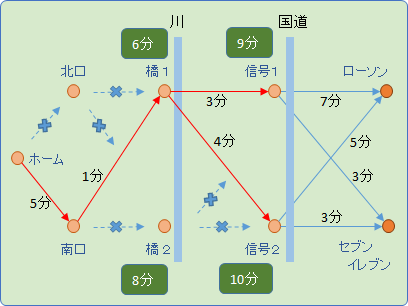
つぎは国道 (信号1、信号2)まで調べます。
ここで前提として、先にもとめた橋1、橋2までの最短経路を使います。それぞれ 6分と 8分でした。
▲ 信号1
橋1まで 6分 そこから信号1 まで 3分 → 計 9分 ⇐ 信号1への最短経路
橋2まで 8分 そこから信号1 まで 2分 → 計 10分 (遠回り。この経路は選択肢からはずす)
▲ 信号2
橋1まで 6分 そこから信号2 まで 4分 → 計 10分 ⇐ 信号2への最短経路
橋2まで 8分 そこから信号2 まで 3分 → 計 11分 (遠回り。この経路は選択肢からはずす)
こうなります。
③ コンビニまで
そして、コンビニまでの最短経路を求めます。
前提は、先にもとめた信号1、信号2までの最短経路を使います。それぞれ 9分と 10分でした。
▲ ローソン
信号1まで 9分 そこからローソン まで 7分 → 16分
信号2まで 10分 そこからローソン まで 5分 → 15分 ⇐ ローソンへの最短経路
▲ セブンイレブン
信号1まで 9分 そこからセブンイレブン まで 3分 → 12分 ⇐ セブンイレブンへの最短経路
信号2まで 10分 そこからセブンイレブン まで 3分 → 13分
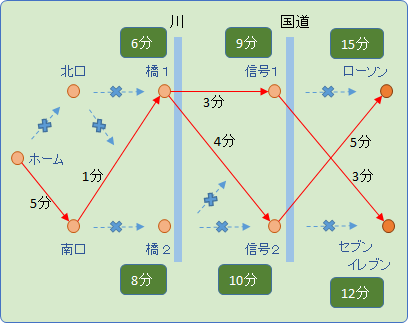
答え
ホーム -> 南口 -> 橋 1 -> 信号1 -> セブンイレブンが最短
最短経路をもとめるとは、つまり
ポイント X までの最短を求めるとします。
- 直前のポイント A、B までの最短時間を A0分、B0分
- A から X までを AX分
- B から X までを BX分
とすると
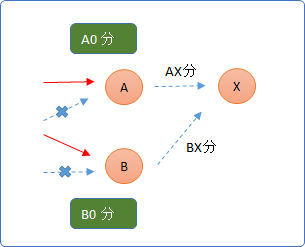
(A0 + AX) と (B0 + BX) を比べて、短いほうが X への最短時間になります。
仮に前者が短かければ、X の直前のポイントは A に決まります。
つまり、「Xへの最短を選ぶ」 という行為は 「Xの直前のポイントを選ぶ 」 という行為に等しいといえます。そして、すべてのポイントにおいて「直前のポイント」を選んで、それを線でつなげば最短経路になるはずです。
プログラムで組んでみる
python で実装
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
import numpy as np names =\ [ [u'北口', u'南口'], [u'橋1', u'橋2'], [u'信号1', u'信号2'], [u'ローソン', u'セブンイレブン'] ] times =\ [ [[3],[5]], [[4,1],[5,4]], [[3,2],[4,3]], [[7,5],[3,3]] ] bfr_pnt = [[0,0],[0,0],[0,0],[0,0]] # 直前のポイント accum_tm = [[0,0],[0,0],[0,0],[0,0]] # 累積時間 for i in range(len(accum_tm)): if i == 0: accum_tm[i][0] = times[i][0][0] accum_tm[i][1] = times[i][1][0] else: # # 橋1、信号1、ローソン # # 「2つの直前ポイントまでの時間 + そこからの時間」 を比較 cmp_0 = [accum_tm[i-1][0] + times[i][0][0], accum_tm[i-1][1] + times[i][0][1]] min_0 = np.argmin(cmp_0) # 短いほう 0 or 1 accum_tm[i][0] = cmp_0[min_0] # 短いほうの時間 bfr_pnt[i][0] = min_0 # 直前のポイント # # 橋2、信号2、セブンイレブン # # 「2つの直前ポイントまでの時間 + そこからの時間」 を比較 cmp_1 = [accum_tm[i-1][0] + times[i][1][0], accum_tm[i-1][1] + times[i][1][1]] min_1 = np.argmin(cmp_1) # 短いほう 0 or 1 accum_tm[i][1] = cmp_1[min_1] # 短いほうの時間 bfr_pnt[i][1] = min_1 # 直前のポイント shortest = np.argmin(accum_tm[3]) print u'%s\t%d分' % (names[3][shortest], accum_tm[3][shortest]) for i in reversed(range(1,len(bfr_pnt))): shortest = bfr_pnt[i][shortest] print u'%s\t%d分' % (names[i-1][shortest], accum_tm[i-1][shortest]) |
出力結果
|
1 2 3 4 |
セブンイレブン 12分 信号1 9分 橋1 6分 南口 5分 |
bfr_pnt、accum_tm はこうなっています。
|
1 2 3 4 5 6 7 8 9 |
bfr_pnt #---------------------------------- # [[0, 0], [1, 0], [0, 0], [1, 0]] #---------------------------------- accum_tm #------------------------------------- # [[3, 5], [6, 8], [9, 10], [15, 12]] #------------------------------------- |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 |
# -*- coding: utf-8 -*- class Path(object): """ 経路 """ def __init__(self, beforePos, nextPos, time): self.beforePos = beforePos self.nextPos = nextPos self.time = time def getTotalTime(self): ''' before までの所要時間 + この経路にかかる時間 ''' # 「before までの所要時間」 が未計算の場合は計算させる。 if (self.beforePos.bestTime is None): self.beforePos.calcBestTime() return self.beforePos.bestTime + self.time class Position(object): """ 場所 """ def __init__(self, name): self.name = name self.beforePathList = [] self.nextPathList = [] self.bestTime = None self.bestPath = None def addNext(self, nextPos, time): """ 次の場所 "next" を追加 """ path = Path(self, nextPos, time) self.nextPathList.append(path) nextPos.addBefore(path) def addBefore(self, path): """ 前の場所 "before" を追加 """ self.beforePathList.append(path) def determineBestPath(self): """ 最適経路をさがす """ self.calcBestTime() def calcBestTime(self): """ 所要時間をもとめ、最適の経路を選択する """ if len(self.beforePathList) == 0: #-------------- # 始点の場合 #-------------- self.bestTime = 0 else: #-------------- # 始点以外 #-------------- # 経路ごとに到達の所要時間をもとめる # getTotalTime() → calcBestTime() → ・・・ と、始点までの再帰呼出しになる times = [path.getTotalTime() for path in self.beforePathList] # 最適経路を選択 (min を max に変えると最長経路) bestTimeIndex = times.index(min(times)) self.bestPath = self.beforePathList[bestTimeIndex] self.bestTime = times[bestTimeIndex] def getBestTime(self): return self.bestTime def getBestPathSeq(self): ''' 最適経路の各ポイントを配列にセット ''' positions = [] self.trackBestPath(positions) positions.reverse() return positions def trackBestPath(self, positions): positions.append(self) if self.bestPath is not None: self.bestPath.beforePos.trackBestPath(positions) if __name__ == "__main__": #========================= # 地図を組み立て #========================= home = Position(u'ホーム') north = Position(u'北口') south = Position(u'南口') bridge1 = Position(u'橋1') bridge2 = Position(u'橋2') cross1 = Position(u'信号1') cross2 = Position(u'信号2') lawson = Position(u'ローソン') seven = Position(u'セブンイレブン') # ホーム ⇒ 北口、南口 home.addNext(north, time=3) home.addNext(south, time=5) # 北口 ⇒ 橋1、橋2 north.addNext(bridge1, time=4) north.addNext(bridge2, time=5) # 南口 ⇒ 橋1、橋2 south.addNext(bridge1, time=1) south.addNext(bridge2, time=4) # 橋1 ⇒ 信号1、信号2 bridge1.addNext(cross1, time=3) bridge1.addNext(cross2, time=4) # 橋2 ⇒ 信号1、信号2 bridge2.addNext(cross1, time=2) bridge2.addNext(cross2, time=3) # 信号1 ⇒ ローソン、セブンイレブン cross1.addNext(lawson, time=7) cross1.addNext(seven, time=3) # 信号2 ⇒ ローソン、セブンイレブン cross2.addNext(lawson, time=5) cross2.addNext(seven, time=3) #========================= # 最短経路を求める #========================= # ローソンまで lawson.determineBestPath() print u'所要時間', lawson.getBestTime(), u'分' print u' -> '.join([pos.name for pos in lawson.getBestPathSeq()]) # セブンイレブンまで seven.determineBestPath() print u'所要時間', seven.getBestTime(), u'分' print u' -> '.join([pos.name for pos in seven.getBestPathSeq()]) |
|
1 2 3 4 |
所要時間 15 分 ホーム -> 南口 -> 橋1 -> 信号2 -> ローソン 所要時間 12 分 ホーム -> 南口 -> 橋1 -> 信号1 -> セブンイレブン |
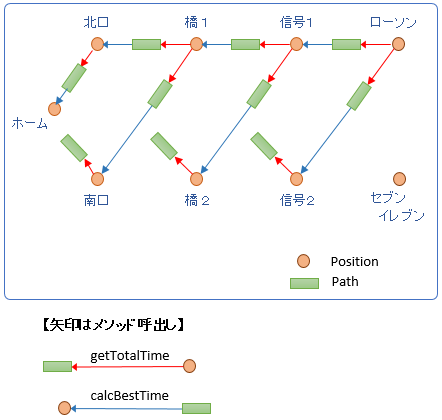
クラスは2つ。
- 場所を表す Position
- 場所をつなぐ Path
Position は自分の直前の Path に計算指示を出し(getTotalTime 呼出し)
Path は自分の直前の Position に計算指示を出す(calcBestTime 呼出し)
再帰呼出しになっています。
後ろのほうから前にむかって計算指示を出し、始点のホームに到達したら、くるりと向きを変えて計算結果を戻していきます。