python でカーブフィッティングをやる関数は1つじゃないようです。次の3つを見つけました。
- Numpy の polyfit
- Scipy の optimize.leastsq
- Scipy の optimize.curve_fit
なぜ3つもあるのか悩みますが、とりあえず使い比べてみました。
機能に違いがあるのか、使いやすいのはどれか・・・
結論を先にいうと、計算結果はほぼ同じ(ごく微小な差異あり)、使い勝手は polyfit が一番簡単でした。
ちなみに、polyfit は最小二乗法によるカーブフィットであることが、こちらに記載されています ⇒ Scipy.org
まず テストデータ
使用するデータは Numpy で生成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import numpy as np from matplotlib import pyplot as plt x = np.array([0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]) y = np.array([-1,-3,-1,9,21,30,37,39,67,65,95,123,142,173,191,216,256,292,328,358]) # y は次の式で生成 # y = np.round(x**2 + np.random.randn(20) * 5) # plt.scatter(x , y) # |
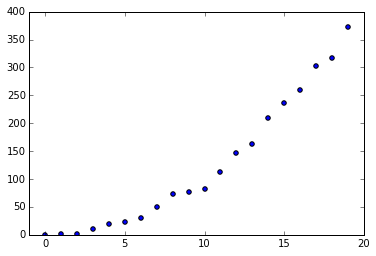
このデータを直線、または曲線で近似しますが、3つの関数でそれぞれ次数を変えながら結果を確認してみます。
次数 2 \(ax^2 + bx + c\)
次数 3 \(ax^3 + bx^2 + cx + d\)
:
曲線の次数があがるほどデータの分布に近づきますが、近ければいいわけでもありません。
polyfitを使ってみる
次数を 1、つまり一次式 \(ax + b\) で近似してみます。
引数の3番目が次数です。
|
1 2 3 4 |
np.polyfit(x, y, 1) #------------------------------------- # array([ 19.39774436, -59.92857143]) #------------------------------------- |
配列が返ってきました。
この戻り値がそのまま 係数 a、b に相当するので
が近似式になります。
この式で 自力で y を計算してもいいのですが poly1d という便利な関数があります。
poly1d
poly1d は、係数 a、b をもとに関数を生成してくれます。
|
1 |
func = np.poly1d(np.polyfit(x, y, 1)) |
この関数に x を渡せば計算までこなしてくれます。
|
1 2 3 4 5 6 7 8 |
func(x) #------------------------------------------------------------------- # array([ -59.92857143, -40.53082707, -21.13308271, -1.73533835, # 17.66240602, 37.06015038, 56.45789474, 75.8556391 , # 95.25338346, 114.65112782, 134.04887218, 153.44661654, # 172.8443609 , 192.24210526, 211.63984962, 231.03759398, # 250.43533835, 269.83308271, 289.23082707, 308.62857143]) #------------------------------------------------------------------- |
一行でまとめると
|
1 |
np.poly1d(np.polyfit(x, y, 1))(x) |
次の一行で、計算 ~ 描画ができてしまいます。
|
1 |
plt.plot(x, np.poly1d(np.polyfit(x, y, 1))(x), label='d=1') |
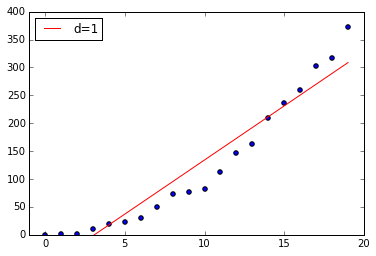
次数を2にすると
polyfit のパラメータを変えるだけで次数は簡単に変更できます。
2次式 \(ax^2 + bx + c\) で近似すると
|
1 2 3 |
plt.plot(x, np.poly1d(np.polyfit(x, y, 2))(x), label='d=2') # ↑ # 次数 |
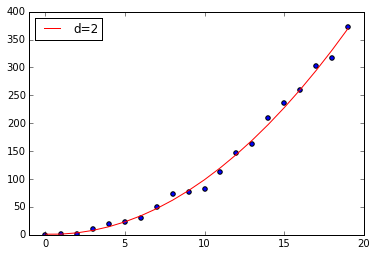
polyfit の戻り値は [ 1.0702324 , -0.93667122, 1.07467532]
つまり、数式は \(y = 1.0702324x^2 – 0.93667122x + 1.07467532\) です。
次数を増やす
次数を 3、5、10、15 とどんどん増やして過学習させると次のようになりました。
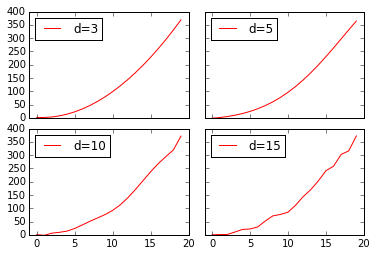
次数 10 や 15 がデータに過剰適応しているのが見て取れます。
数式を導き出すさい、特定の学習データ(この場合、x と y)に近づけすぎて、一般的な予測モデルとして使えなくなること。
たとえば、次数 15 の近似式は学習データに近づこうとするあまり、データの偏りに強くひきづられている。そのため、新たなデータとして x=n を与えても、計算結果 y は予測値として信頼がおけない。
leastsqを使ってみる
leastsq で近似してみます。
(polyfit、curve_fit との比較結果をページ後半に載せてあります)
次数 1
|
1 2 3 4 5 6 7 8 9 10 11 |
from scipy import optimize def func1(param,x,y): residual = y - (param[0]*x + param[1]) return residual param1 = [0, 0] optimize.leastsq(func1, param1, args=(x, y)) #-------------------------------------------- # (array([ 19.39774436, -59.92857143]), 1) #-------------------------------------------- |
結果:\(y = 19.39774436x – 59.92857143\)
次数 2
|
1 2 3 4 5 6 7 8 9 |
def func2(param,x,y): residual = y - (param[0]*x**2 + param[1]*x + param[2]) return residual param2 = [0, 0, 0] optimize.leastsq(func2, param2, args=(x, y)) #-------------------------------------------------------- # (array([ 1.07023241, -0.93667149, 1.07467603]), 1) #-------------------------------------------------------- |
結果:\(y = 1.07023241x^2 – 0.93667149x + 1.07467603\)
次数 3
|
1 2 3 4 5 6 7 8 9 |
def func3(param,x,y): residual = y - (param[0]*x**3 + param[1]*x**2 + param[2]*x + param[3]) return residual param3 = [0, 0, 0, 0] optimize.leastsq(func3, param3, args=(x, y)) #------------------------------------------------------------------ # (array([-0.00231212, 1.13612786, -1.42475939, 1.74680471]), 1) #------------------------------------------------------------------ |
結果:\(y = -0.00231212x^3 + 1.13612786x^2 – 1.42475939x + 1.74680471\)
curve_fitを使ってみる
curve_fit で近似してみます。
(polyfit、leastsq との比較結果をページ後半に載せてあります)
次数 1
|
1 2 3 4 5 6 7 8 9 |
def func_c1(x, a, b): return a*x + b optimize.curve_fit(func_c1, x, y) #--------------------------------------------- # (array([ 19.39774436, -59.92857143]), # array([[ 1.77304484, -16.84392603], # [ -16.84392603, 218.97103783]])) #--------------------------------------------- |
結果:\(y = 19.39774436x – 59.92857143\)
次数 2
|
1 2 3 4 5 6 7 8 9 10 |
def func_c2(x, a, b, c): return a*x**2 + b*x + c optimize.curve_fit(func_c2, x, y) #------------------------------------------------------------------ # (array([ 1.0702324 , -0.93667122, 1.07467532]), # array([[ 3.73510483e-03, -7.09669890e-02, 2.12900904e-01], # [ -7.09669890e-02, 1.44697961e+00, -4.98188229e+00], # [ 2.12900904e-01, -4.98188229e+00, 2.43132932e+01]])) #------------------------------------------------------------------ |
結果:\(y = 1.0702324x^2 – 0.93667122x + 1.07467532\)
次数 3
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
def func_c3(x, a, b, c, d): return a*x**3 + b*x**2 + c*x +d optimize.curve_fit(func_c3, x, y) #------------------------------------------------------------------ # (array([-0.00231212, 1.13612793, -1.42476056, 1.74680971]), # array([[ 1.57550850e-04, -4.49019885e-03, 3.32589797e-02, # -4.58000146e-02], # [ -4.49019885e-03, 1.31930807e-01, -1.02312372e+00, # 1.53102892e+00], # [ 3.32589797e-02, -1.02312372e+00, 8.55513261e+00, # -1.49504332e+01], # [ -4.58000146e-02, 1.53102892e+00, -1.49504332e+01, # 3.90922788e+01]])) #------------------------------------------------------------------ |
結果:\(y = -0.00231212x^3 + 1.13612793x^2 – 1.42476056x + 1.74680971\)
比べてみる
関数3つの結果を表にしました。次数は1~3です。
polyfit と curve_fit は値が完全に同じです。leastsq は、10 の-5乗あたりで他の2つと差が出るケースがあるようですが、実際上は同じと考えてよさそうです。
次数 1
\(y = ax + b\)
| a | b | |
| polyfit | 19.39774436 | -59.92857143 |
| leastsq | 19.39774436 | -59.92857143 |
| curve_fit | 19.39774436 | -59.92857143 |
次数 2
\(y = ax^2 – bx + c\)
| a | b | c | |
| polyfit | 1.0702324 | -0.93667122 | 1.07467532 |
| leastsq | 1.07023241 | -0.93667149 | 1.07467603 |
| curve_fit | 1.0702324 | -0.93667122 | 1.07467532 |
次数 3
\(y = ax^3 – bx^2 + cx + d\)
| a | b | c | d | |
| polyfit | -0.00231212 | 1.13612793 | -1.42476056 | 1.74680971 |
| leastsq | -0.00231212 | 1.13612786 | -1.42475939 | 1.74680471 |
| curve_fit | -0.00231212 | 1.13612793 | -1.42476056 | 1.74680971 |
匿名 says:
こんにちは。いつもお世話になっております。^^
これらのコードの続きで、決定係数、R2を求めるコードってどんな感じでしょうか?回答頂けましたら幸いです。どうぞよろしくお願い申し上げます。
秋雪 says:
分かりやすい内容で助かっております。ありがとうございます。
一点だけ、
「次数 10 や 15 がデータに過剰適応しているのが見て取れます。」
までは良いのですが、
「過学習:数式を導き出すさい、特定の学習データ(この場合、x と y)に近づけすぎて・・・」との記述部分は、今回の記事にそぐわないように思います。そもそも機械学習とか深層学習のように「学習させて」フィッティングせずに「polyfitで厳密に決定」されています。
あくまで、人間側が次数のモデルを予測して選択する範疇なので、「過剰適応してしまうモデルを選択すると良くない。」といった表現が適切に思えました。