ロジスティック回帰の2クラス分類を Chainer と TensorFlow でやってみます。
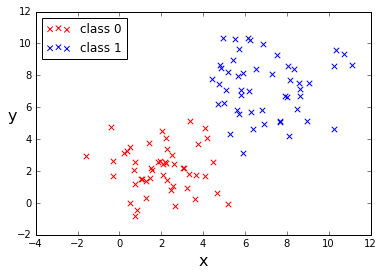
データは \(x,y\) の 2次元とし、下図のように赤と青のグループを生成します。それぞれ クラス 0、クラス 1 とし、両クラスをうまく分類できそうな境界線を Chainer と TensorFlow で探します。
ロジスティック回帰の(超)概要
ロジスティック回帰の詳細は専門の書籍なり Web を見てもらうしかありませんが、端折りに端折って説明するとこうなります。
\(x,y\) を \(w_1x+w_2y+bias\) と線形変換し、その値をシグモイド関数
に代入します。得られた値 \(p\) は 0~1 の実数値をとりますが、この値を確率値とみなします。なんの確率かというと \(x,y\) がクラス 1である確率 です。
なぜ、この値が確率になるのか
もちろん、ただ計算するだけではまともな確率は求まりません。そもそも \(w_1, w_2, bias\) の値がどうなっているのか不明ですから、そんなよく判らない係数で計算しても、出てくる値はでたらめです。そこで、どうするかというと \(w_1, w_2, bias\) を調整してやります。確率をうまく計算できるように調整してやるわけです。
どのように調整するか
まず正解のデータを用意しておきます。正解とは、実際のクラス(0 または 1)のことです。実際のクラス(0 または 1)を事前に確認しておき、それを正解 \(t\) とします。
計算した確率 \(p\) (0~1)と 正解 \(t\) (0 または 1)が一致するかどうかは \(w_1, w_2, bias\) 次第です。\(p\) と \(t\) がなるべく多くののデータで一致するように、上手に \(w_1, w_2, bias\) を求めるのがロジスティック回帰です。
うまく調整するには数学的な手順が必要ですが Chainer や TensorFlow はその辺をすべてやってくれるので、自力でロジックを組む必要はありません。
Chainer で
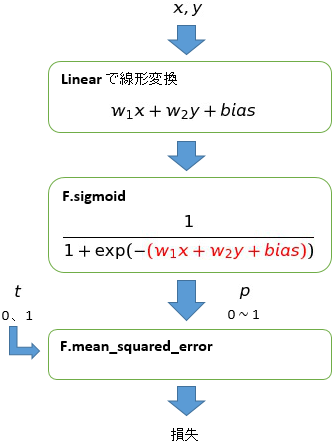
Chainer では数式が表にでてきませんが、Linear クラスで線形変換 \(w_1x+w_2y+bias\) を行い、その出力を活性化関数 F.sigmoid に与えます。sigmoid の出力が上式の \(\small{P(x,y)}\) に相当し、その値を二乗平均誤差の関数 F.mean_squared_error に渡して損失を求めます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
import matplotlib.pyplot as plt import numpy as np import chainer.functions as F import chainer.links as L from chainer import Chain, optimizers, Variable from sklearn.preprocessing import StandardScaler class Model(Chain): def __init__(self): super(Model, self).__init__( l1=L.Linear(2, 1), ) def __call__(self, x): return F.sigmoid(self.l1(x)) # # データ生成 # np.random.seed(seed=0) xy_0 = np.random.multivariate_normal( [2,2], [[2,0],[0,2]], 50 ) t_0 = np.zeros(len(xy_0)) xy_1 = np.random.multivariate_normal( [7,7], [[3,0],[0,3]], 50 ) t_1 = np.ones(len(xy_1)) xy_all = np.vstack((xy_0, xy_1)) t_all = np.append(t_0, t_1).reshape(-1,1) train_data = np.random.permutation(np.hstack((xy_all, t_all))) train_xy = train_data[:,[0,1]].astype(np.float32) train_t = train_data[:,2].reshape(-1,1).astype(np.float32) # # データを標準化(平均 0、標準偏差 1) # sc = StandardScaler() train_xy = sc.fit_transform(train_xy) # # モデル生成 # model = Model() optimizer = optimizers.Adam() optimizer.setup(model) # # 学習 # for i in range(3000): optimizer.zero_grads() p = model(Variable(train_xy)) loss = F.mean_squared_error(p, Variable(train_t)) loss.backward() # 誤差逆伝播 optimizer.update() if i % 500 == 0: acc = ((p.data > 0.5) == (train_t > 0.5)).sum() / len(p) print (loss.data, acc) # # 学習結果の重みとバイアスを取りだす # w_1, w_2 = model.l1.W.data[0] bias = model.l1.b.data[0] plt.title('Chainer (loop:{0})'.format(i+1)) plt.plot([min(train_xy[:,0]),max(train_xy[:,0])], list(map(lambda x: (-w_1 * x - bias)/w_2, [min(train_xy[:,0]),max(train_xy[:,0])]))) plt.scatter(train_xy[train_t.ravel()==0, 0], train_xy[train_t.ravel()==0, 1], c='red', marker='x', s=30, label='train 0') plt.scatter(train_xy[train_t.ravel()==1, 0], train_xy[train_t.ravel()==1, 1], c='blue', marker='x', s=30, label='train 1') plt.legend(loc='upper left') |
TensorFlow で
TensorFlow の場合、線形変換や損失の計算式を自前で定義します。損失は次の式で求めます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
import matplotlib.pyplot as plt import tensorflow as tf import numpy as np from sklearn.preprocessing import StandardScaler # # データ生成 # np.random.seed(seed=0) xy_0 = np.random.multivariate_normal( [2,2], [[2,0],[0,2]], 50 ) t_0 = np.zeros(len(xy_0)) xy_1 = np.random.multivariate_normal( [7,7], [[3,0],[0,3]], 50 ) t_1 = np.ones(len(xy_1)) xy_all = np.vstack((xy_0, xy_1)) t_all = np.append(t_0, t_1).reshape(-1,1) train_data = np.random.permutation(np.hstack((xy_all, t_all))) train_xy = train_data[:,[0,1]] train_t = train_data[:,2].reshape(-1,1) # # データを標準化(平均 0、標準偏差 1) # sc = StandardScaler() train_xy = sc.fit_transform(train_xy) # # TensorFlow の各種定義 # xy = tf.placeholder(tf.float32, [None, 2]) t = tf.placeholder(tf.float32, [None, 1]) w = tf.Variable(tf.zeros([2, 1])) b = tf.Variable(tf.zeros([1])) f = tf.matmul(xy, w) + b # 線形変換 p = tf.sigmoid(f) # シグモイド関数 loss = tf.reduce_mean(tf.square(p - t)) # 損失 #loss = -tf.reduce_sum(t*tf.log(p) + (1-t)*tf.log(1-p)) train_step = tf.train.AdamOptimizer().minimize(loss) sess = tf.Session() sess.run(tf.global_variables_initializer()) # # 学習 # for i in range(3000): sess.run(train_step, feed_dict={xy:train_xy, t:train_t}) if i % 500 == 0: p_val, loss_val = sess.run([p, loss], feed_dict={xy:train_xy, t:train_t}) acc = ((p_val > 0.5) == (train_t > 0.5)).sum() / len(p_val) print (loss_val, acc) # # 学習結果の重みとバイアスを取りだす # bias = sess.run(b)[0] w_1, w_2 = sess.run(w)[:,0] plt.title('TensorFlow (loop:{0})'.format(i+1)) plt.plot([min(train_xy[:,0]),max(train_xy[:,0])], list(map(lambda x: (-w_1 * x - bias)/w_2, [min(train_xy[:,0]),max(train_xy[:,0])])),c='green') plt.scatter(train_xy[train_t.ravel()==0, 0], train_xy[train_t.ravel()==0, 1], c='red', marker='x', s=30, label='class 0') plt.scatter(train_xy[train_t.ravel()==1, 0], train_xy[train_t.ravel()==1, 1], c='blue', marker='x', s=30, label='class 1') plt.legend(loc='upper left') |
結果
同じデータを使って、3000回ループさせた結果です。上が Chainer、下が TensorFlow です。
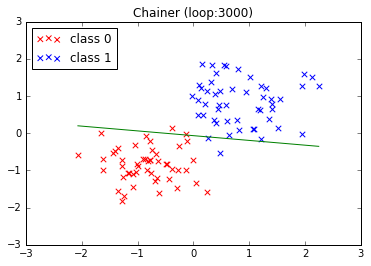
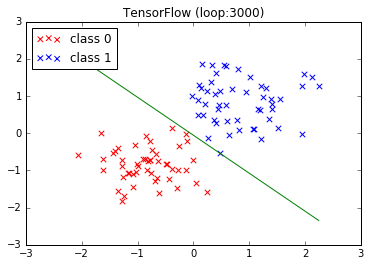
なんか、TensorFlow のほうがいい感じになっています。
Chainer のループを増やしてみる
ループが 3000回だと Chainer の結果がイマイチだったので、ループ回数を増やしてみました。思いきって1万回まわした結果です。
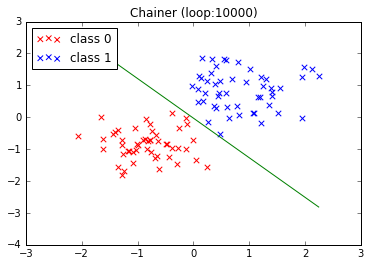
TensorFlow の結果とほぼ同じになりました。
おわり
TensorFlow のほうが良い結果になりましたが、あくまで単純なデータを単純なモデルでパラメータも特に指定せずに実行した結果です。
匿名 says:
2つのフレームワークを比較するなら、
損失関数をどちらかに合わせたほうが良いのでは?
平均二乗誤差にしてもクロスエントロピーにしても。
管理人 says:
なるほど、そうですね。
ご指摘ありがとうございます。m(_ _)m
TensorFlow も平均二乗誤差にしてみました。
(結果は同じでした)
diesel spare parts says:
kusursuz aynı iş merkezi okunuşu fazla memnunuz sizden. Her madde
eksiksiz görünüyor. filhakika sitenizi yetişmek ediyorum.
Custom Basketball Gear Sialkot, Custom Apparel of Basketball, Custom Apparel of Poshline as Suppliers,CZ Boxing Review as Poshline Company says:
E-mail info@poshlineco.com