多次元正規分布を Numpy の multivariate_normal で取得し、Axes3D で描画してみます。
- 目次 -
スポンサーリンク
Numpy の multivariate_normal について
multivariate_normal に 平均 と 共分散行列 を指定すると多次元正規分布の乱数を生成してくれます。
2次元の場合
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import numpy as np # 平均 共分散行列 データ数 # ↓ ↓ ↓ np.random.multivariate_normal( [2,2], [[1,0],[1,2]], 5 ) #------------------------------------ # array([[-0.47483069, 2.36246966], # [ 2.46683508, 1.85869577], # [ 2.39708925, 5.01841042], # [ 1.07742266, 0.2697148 ], # [ 1.49281663, 1.85296466]]) #------------------------------------ |
3次元の場合
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import numpy as np # 平均 共分散行列 データ数 # ↓ ↓ ↓ np.random.multivariate_normal( [2,2,2], [[1,0,0],[1,2,2],[0,0,2]], 5 ) #-------------------------------------------------- # array([[ 2.75291822, 4.62329366, 2.21681943], # [ 1.14062016, -0.65898867, -0.18007289], # [ 2.99782411, 2.30250398, 4.23673396], # [ 0.93594171, 0.18373579, 1.6584117 ], # [ 1.25846541, 3.65604433, 2.4874375 ]]) #-------------------------------------------------- |
ソース
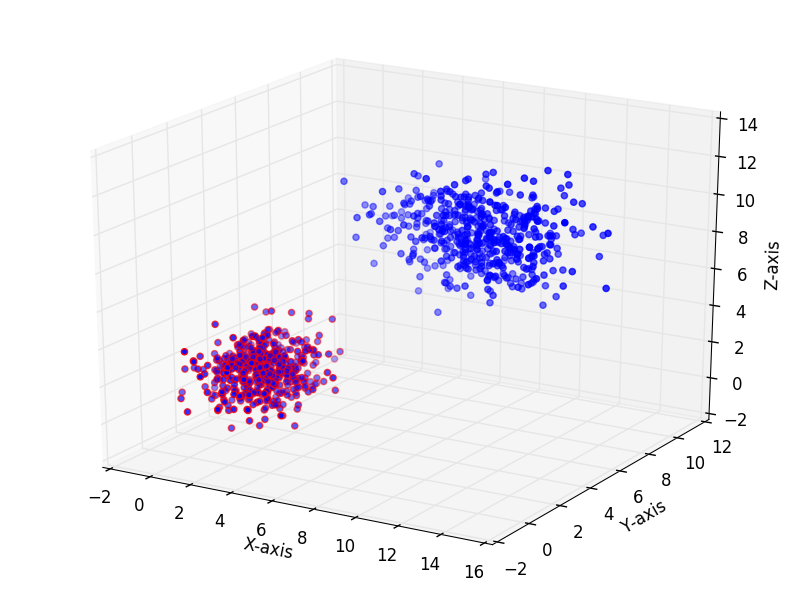
平均、共分散の異なる乱数群を 2 つ取得し、描画します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D size = 500 # 平均 mean_1 = [2, 2, 2] mean_2 = [8, 8, 8] # 共分散 cov_1 = [[1, 0, 0], [0, 1, 0], [0, 0, 1]] cov_2 = [[5, 0, 0], [0, 0.5, 0], [0, 0, 2]] # 乱数を生成 data_1 = np.random.multivariate_normal(mean_1, cov_1, size) data_2 = np.random.multivariate_normal(mean_2, cov_2, size) # # 描画 # fig = plt.figure() ax = Axes3D(fig) ax.set_xlabel("X-axis") ax.set_ylabel("Y-axis") ax.set_zlabel("Z-axis") ax.scatter(data_1[:,0], data_1[:,1], data_1[:,2], color='r') ax.scatter(data_2[:,0], data_2[:,1], data_2[:,2], color='b') plt.show() |