回転行列をベクトルにかけあわせると、ベクトルが回転します。回転する角度を θ とすると、2次元の回転行列は次の通りです。
\(
\left(
\begin{array}{cc}
cos \theta & -sin \theta \\
sin \theta & cos \theta
\end{array}
\right)
\)
\left(
\begin{array}{cc}
cos \theta & -sin \theta \\
sin \theta & cos \theta
\end{array}
\right)
\)
これでどうして回転するのかパッと見よくわかりませんが、仕組みを理解するため求め方を考えてみます。
- 目次 -
スポンサーリンク
求めかた
下図のように 緑のベクトル を θ 度回転させ、オレンジ の位置に移動したとします。
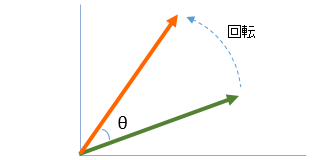
緑のベクトル の成分を (n、m) とします。
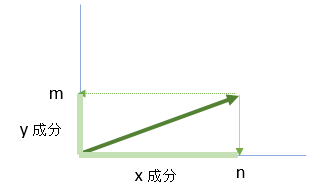
ベクトルの回転にあわせて、x成分、y成分 も回転させてみます。すると下図のようになります。回転後の x成分、y成分 の位置を n´、m´ とします。
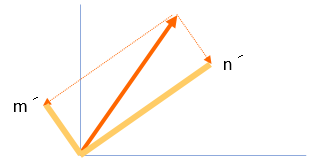
ここで n´、m´ の座標はどうなるのか考えます。それが判れば、回転後のベクトル成分が判ります。なぜなら、 n´、m´ をベクトルと考えると、n ´ + m´ が回転後のベクトルの終点だからです。
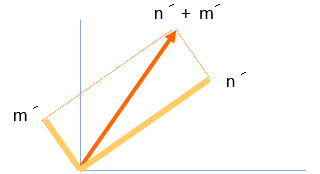
n´、m´を確認するため、回転前後の x成分、y成分 を並べてみます。
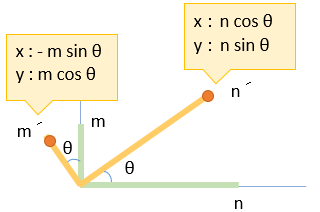
上図のとおり、
n´ の座標は
m´ の座標は
m´ の座標は
n cos θ
– m sin θ
– m sin θ
、
、
、
n sin θ
m cos θ
m cos θ
です。
そして、先に述べましたが、回転後のベクトルの終点は n ´ + m´ です。

n ´ + m´ を計算すると
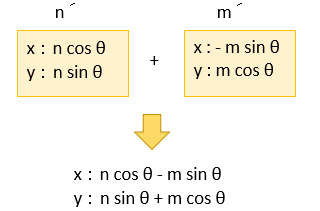
つまり、回転前、後のベクトルはこうなります。
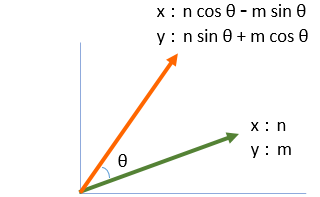
行列の計算式になおすと、回転後のベクトルはこうなります。
\(
\left(
\begin{array}{cc}
cos \theta & -sin \theta \\
sin \theta & cos \theta
\end{array}
\right)
\left(
\begin{array}{c}
n \\
m
\end{array}
\right)
\)
\left(
\begin{array}{cc}
cos \theta & -sin \theta \\
sin \theta & cos \theta
\end{array}
\right)
\left(
\begin{array}{c}
n \\
m
\end{array}
\right)
\)
左側にでてきたのが 回転行列 です。
たなか says:
回転行列がなぜそうなっているか理解できて面白かったです。
管理人 says:
たなかさん
コメント有難うございます。
線形代数の本を何冊か見ても、説明がなかったので作ってみました。
匿名 says:
分かりやすくて脳汁出ました
管理人 says:
脳汁(笑)
匿名 says:
「あぁ~おぉ~~」と声が出ました。とてもわかりやすかったです。
管理人 says:
ありがとうございます
匿名 says:
わかりやすい説明ありがとうございます。
1点だけ質問させていただきたいのですが、m'の座標はx = -msinθ, y = mcosθとなっていますが、
なぜこうなるのでしょうか?
x = mcosθ, y = msinθになるように思っておりました・・・。
匿名 says:
ただ単純にm'が第2象限にあるので、xはマイナスの値になると理解しました。
匿名 says:
わかりやすすぎる!
初めて理解しました!ありがとうございます!
masa says:
すごいわかりやすいです。
匿名 says:
分かりやすいです。天才。
匿名 says:
回転が納得できました。
感謝です。
ななな says:
直感的に理解出来た。ありがとう。