シグモイド関数の傾きやバイアスについて見ていきます。
- 目次 -
スポンサーリンク
傾きとバイアスを変えるには
傾きとバイアスがどのように変わるか見てみます。
まず、シグモイド関数の確認。
\(\small{S(x)=} \large\frac{1}{1+ \exp (-x)} \)
こんな式です。
で、
この式の変数は \(x\) ですが、この \(x\) を次のように \(ax+b\) と書きかえます。
\(\small{S(x)=} \large\frac{1}{1+ \exp (-(ax+b))} \)
入力 \(x\) を a倍 し、そこに定数 b を加算 してから式に代入するわけですが、この式で a を変えると傾きが変化 し、b を変えるとバイアスが変化 します。
a
b
機械学習で
シグモイド関数は機械学習でよく使われますが、学習で求めるのは a と b 、つまり傾きとバイアスを変化させる値です。ディープラーニングの活性化関数となる場合も同様で、下図のように線形変換の結果 \(ax+b\) が求めれら、その値がシグモイド関数の入力となります。
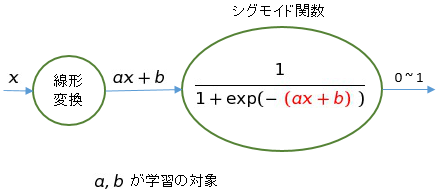
学習で求めるのは線形変換の a と b ですが、それはシグモイド関数の傾きとバイアスを学習させているとも言えます。
resweatr says:
スライダーでaとbを変化させるとグラフもリアルタイムに変化する。とても直観的で理解が深まりました。ありがとうございます。
今はシグモイド関数の理解をしなきゃいけないのですが、どうやって作ったのかも気になって仕方がありません。こうしたものは、なにかのJSライブラリで作れるのでしょうか?!
pillo says:
コメント失礼します。
このa,bを導出する式などはありますでしょうか?