二項分布と多項分布の初歩


二項分布 と 多項分布 の初歩的な考え方をまとめてみました。

- 目次 -

スポンサーリンク

二項分布

コインを３回投げて、それぞれ表がでたか裏がでたかを記録します。
コインには細工がしてあり、表の出る確率は 70% 、裏の出る確率は 30%とします。

問題
３回投げて、表が２回、裏が１回となる確率は？

やりがちな間違い
確率 = 0.7 × 0.7 × 0.3
という答えがぱっと思いつきますが、これは間違いです。

なぜ、間違いなのか
コインの裏表のパターンは下図のように８通りです。
この８通りのうち、0.7 × 0.7 × 0.3 で求まるのは赤い部分だけです。

nikou

70% が２回、30% が１回というのは \( 0.7^{2} \times 0.3^{1} \) ですが、上図からわかるように、それが３通りのパターンでありえます（赤字と青字の部分）。

したがって、問題に対する答えは

確率 = \(3 \times 0.7^{2} \times 0.3^{1} \)

となります。

注
問題がもし、表 → 表 → 裏の 順番で出る確率 を問うものなら 0.7 × 0.7 × 0.3 で正解です。順番を問わない問題なので、順番違いの 3パターンを 1つにまとめる必要があります。

3 の求め方
3通りあるから 3 を掛けましたが、この 3 という数字を数式で表すとどうなるかというと、3個から 2個を選択する組合せの数に相当します。

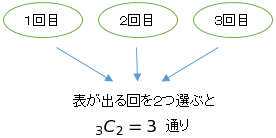
nikou

（3個から 1個を選択する組合せでもOK。同じことです）

これを踏まえて答を書きなおすとこうなります。

確率 = \(_3 C _2 \times 0.7^{2} \times 0.3^{1}\)

公式

上の式を公式として一般化すると

確率 P
\(=\ _n C _r \ \theta_1^{r} \ \theta_2^{n-r} \)
\(=\large{\frac{n!}{(n-r)!(r)!}} \normalsize{\ \theta_1^{r} \ \theta_2^{n-r}}\)

となります。

\(n\): 投げた回数
\(r\): 表の回数
\(\theta_1\): 表の出る確率
\(\theta_2\): 裏の出る確率

多項分布

多項分布の場合も考え方は同じです。

３面サイコロを６回投げて、出た目を記録します。サイコロには細工がしてあり、1、2、3 の出る確率を 50％、30%、20% とします。

問題
1 が３回、2 が2回、3 が１回となる確率は？

求め方
1 が３回、2 が2回、3 が１回となるパターンが何通りあるかを求め、そのパターン数に \(0.5^{3} \times 0.3^{2} \times 0.2^{1}\) を掛けてやります。

まずパターン数から

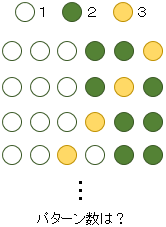
takou

① ６個 から ３個 を取りだす組み合せは \(_6 C _3\)
② 残り３個 から ２個を取りだす組み合せは \(_3 C _2\)
③ 残り１個 から １個 を取りだす組み合せは \(_1 C _1\)

この３つを掛けた値がパターン数です。

パターン数
\(=\ _6 C _3 \times _3 C _2 \times _1 C _1\)
\(=\large{\frac{6!}{3!\ 3!} \times \frac{3!}{1!\ 2!} \times \frac{1!}{0!\ 1!}}\)
\(=\large{ \frac{6!}{3!\ 2!\ 1!}}\)

答
パターン数に \(0.5^{3} \times 0.3^{2} \times 0.2^{1}\) を掛けた値が答なので

確率 = \(\large{ \frac{6!}{3!\ 2!\ 1!}} \normalsize{\times 0.5^{3} \times 0.3^{2} \times 0.2^{1}}\)

公式

上の式を公式として一般化すると

確率 P = \(\large{\frac{n!}{n_1! \cdots n_m!}} \normalsize{\theta_1^{n_1} \cdots \theta_m^{n_m}}\)

\(n\): 投げた回数
\(m\): 目の数（３面なら３、６面なら６）
\(n_i\): \(i\) の出た回数
\(\theta_i\): \(i\) の出る確率

スポンサーリンク
その他の記事

コメントはお気軽に