書籍 Python機械学習プログラミング 達人データサイエンティストによる理論と実践
標準化と正規化
標準化と正規化の計算式はこうなります。
標準化の式
\(x_{std}^{(i)}= \large{\frac{x^{(i)}- \mu}{\sigma}}\)
正規化の式
\(x_{norm}^{(i)}= \large{\frac{x^{(i)}-x_{min}}{x_{max}-x_{min}}} \)
scikit-learn で
sklearn の StandardScaler と MinMaxScaler がそれぞれ 標準化 と 正規化 のモジュールです。主に使うメソッドは次の 3 つです。
- fit
パラメータ（平均や標準偏差 etc）計算 - transform
パラメータをもとにデータ変換 - fit_transform
パラメータ計算とデータ変換をまとめて実行
テスト
２次元のデータで試してみます。２次元正規分布の乱数を 50 個用意し、標準化、正規化を行っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
import matplotlib.pyplot as plt import numpy as np from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import MinMaxScaler # 元データ np.random.seed(seed=1) data = np.random.multivariate_normal( [5, 5], [[5, 0],[0, 2]], 50 ) # 標準化 sc = StandardScaler() data_std = sc.fit_transform(data) # 正規化 ms = MinMaxScaler() data_norm = ms.fit_transform(data) # プロット min_x = min(data[:,0]) max_x = max(data[:,0]) min_y = min(data[:,1]) max_y = max(data[:,1]) plt.figure(figsize=(5, 6)) plt.subplot(2,1,1) plt.title('StandardScaler') plt.xlim([-4, 10]) plt.ylim([-4, 10]) plt.scatter(data[:, 0], data[:, 1], c='red', marker='x', s=30, label='origin') plt.scatter(data_std[:, 0], data_std[:, 1], c='blue', marker='x', s=30, label='standard ') plt.legend(loc='upper left') plt.hlines(0,xmin=-4, xmax=10, colors='#888888', linestyles='dotted') plt.vlines(0,ymin=-4, ymax=10, colors='#888888', linestyles='dotted') plt.subplot(2,1,2) plt.title('MinMaxScaler') plt.xlim([-4, 10]) plt.ylim([-4, 10]) plt.scatter(data[:, 0], data[:, 1], c='red', marker='x', s=30, label='origin') plt.scatter(data_norm[:, 0], data_norm[:, 1], c='green', marker='x', s=30, label='normalize') plt.legend(loc='upper left') plt.hlines(0,xmin=-4, xmax=10, colors='#888888', linestyles='dotted') plt.vlines(0,ymin=-4, ymax=10, colors='#888888', linestyles='dotted') |
結果
実行すると以下の２つの図が表示されます。上が標準化、下が正規化の結果です。
（赤 が元データ、青 が標準化後のデータ、緑 が正規化後のデータ）
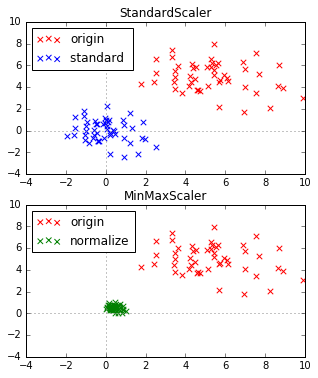
標準化の結果、平均が （0,0）へ移動し、標準偏差が x軸、y軸とも 1 になっています。
|
1 2 3 4 |
data_std[:,0].mean() # => -6.0618177144533547e-16 data_std[:,1].mean() # => -6.3948846218409014e-16 data_std[:,0].std() # => 0.99999999999999978 data_std[:,1].std() # => 0.99999999999999989 |
正規化のほうは、全データが x軸、y軸とも 0~1 に収まっています。
|
1 2 3 4 |
data_norm[:,0].min() # => 0.0 data_norm[:,0].max() # => 0.99999999999999978 data_norm[:,1].min() # => 0.0 data_norm[:,1].max() # => 1.0 |
標準化の効果を確認
以前、こちら の記事で TensorFlow を使ってロジスティック回帰を実行してみました。この時はデータを標準化して実行したのですが、ここでは試しに標準化しない場合はどうなるのか見てみます。下図、赤と青の２種類のデータをうまく分割する線を探しています。
標準化 あり
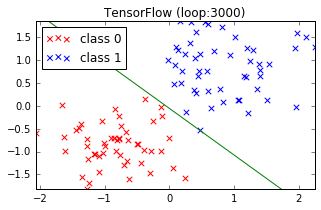
標準化 なし
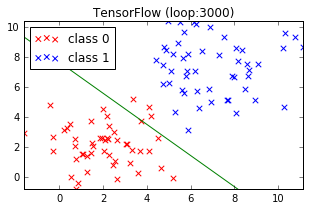
標準化を行った上図のほうがきれいにデータを分割できています。
ついでに標準化と正規化の効果を比較
標準化（再掲）
正規化
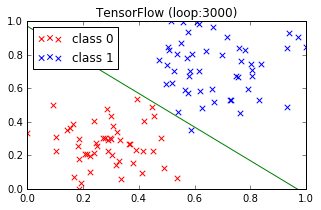
微妙に違います。どっちがいいのか・・・
とりあえず、学習データをうまく分割できたのは標準化したほうです。検証データを別に用意して試せばどうなるかちょっと判りませんが。